Embark on a journey of geometric precision as we delve into the intricacies of parallel and perpendicular lines. This comprehensive guide to the Unit 3 Test Parallel and Perpendicular Lines Answer Key will equip you with the knowledge and understanding to conquer any challenge.
Within these pages, you will find a wealth of information, including clear definitions, insightful explanations, and a meticulously crafted answer key. Prepare to enhance your geometric prowess and excel in your upcoming assessment.
Unit 3 Test on Parallel and Perpendicular Lines
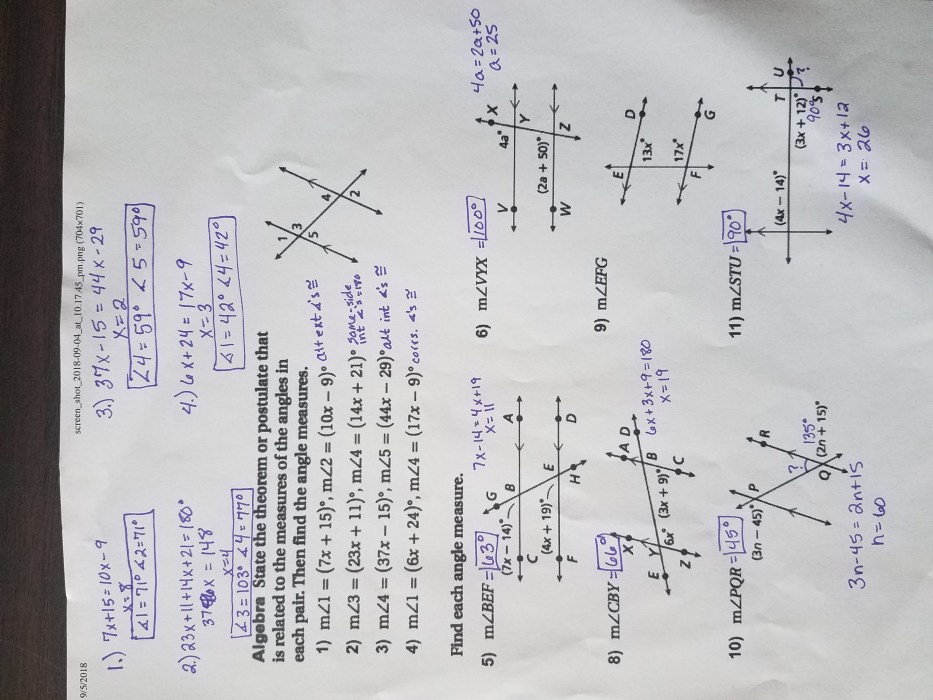
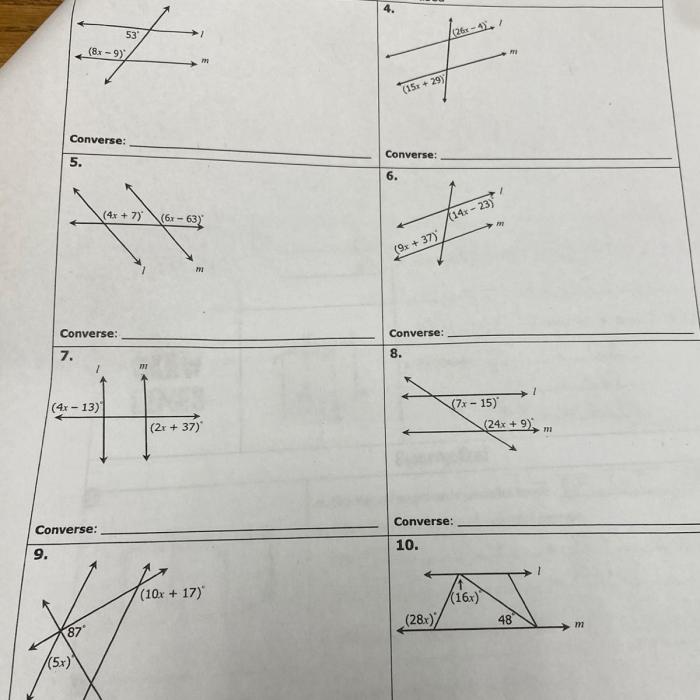
In geometry, parallel and perpendicular lines are fundamental concepts that describe the relationships between lines in a plane. Understanding these concepts is essential for solving various geometry problems and applications in real-world scenarios.
This unit 3 test aims to assess students’ comprehension of parallel and perpendicular lines. The test will cover the definitions, properties, and relationships between these lines, as well as their applications in solving geometry problems.
Key Concepts
- Parallel Lines:Lines that never intersect and maintain the same distance apart throughout their length.
- Perpendicular Lines:Lines that intersect at a right angle (90 degrees).
Properties of Parallel Lines:
- The distance between parallel lines remains constant.
- Alternate interior angles formed by a transversal are congruent.
- Corresponding angles formed by a transversal are congruent.
Properties of Perpendicular Lines:
- The angle formed by two perpendicular lines is 90 degrees.
- Perpendicular lines intersect at a single point.
Relationships between Parallel and Perpendicular Lines:
- Perpendicular lines to the same line are parallel to each other.
- If two lines are perpendicular to a third line, then they are parallel to each other.
Test Content
The unit 3 test will include the following types of questions:
- Identifying parallel and perpendicular lines from diagrams.
- Determining the relationships between lines based on their orientations.
- Solving geometry problems involving parallel and perpendicular lines.
- Applying the properties of parallel and perpendicular lines to solve real-world problems.
Example Problems:
- Find the distance between two parallel lines if the distance between their closest points is 5 cm.
- Determine whether the following lines are parallel, perpendicular, or neither: y = 2x + 3 and y = -2x + 1.
Study Tips, Unit 3 test parallel and perpendicular lines answer key
To prepare effectively for the unit 3 test, consider the following study tips:
- Review the definitions and properties of parallel and perpendicular lines.
- Practice identifying parallel and perpendicular lines from diagrams.
- Solve numerous geometry problems involving parallel and perpendicular lines.
- Pay attention to the relationships between parallel and perpendicular lines.
Common Mistakes to Avoid:
- Assuming that all lines that do not intersect are parallel.
- Mistaking parallel lines for perpendicular lines and vice versa.
- Incorrectly applying the properties of parallel and perpendicular lines.
Answers to Common Questions: Unit 3 Test Parallel And Perpendicular Lines Answer Key
What is the difference between parallel and perpendicular lines?
Parallel lines never intersect, while perpendicular lines intersect at a right angle (90 degrees).
How do I identify parallel and perpendicular lines in a diagram?
Parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals of each other.
What are some common mistakes to avoid when solving problems involving parallel and perpendicular lines?
Common mistakes include assuming that all lines are parallel or perpendicular, not checking for special cases (e.g., vertical or horizontal lines), and making algebraic errors when calculating slopes.