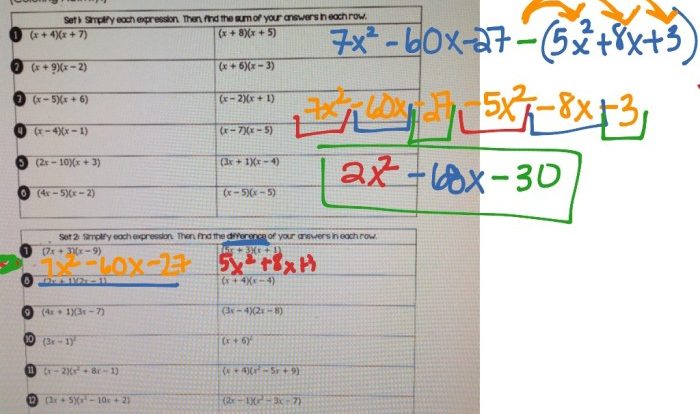
Assume that the radius r of a sphere is expanding – Assuming that the radius r of a sphere is expanding, this article explores the consequences of this phenomenon on various properties of the sphere, including surface area, volume, density, and pressure. The relationships between these properties and the expanding radius will be examined, providing insights into the behavior of expanding spherical systems.

The implications of an expanding radius extend beyond the sphere itself, affecting the surrounding environment and potential applications. By understanding the changes that occur as the radius expands, we gain a deeper understanding of the dynamics of spherical systems and their behavior in various contexts.

Expanding Radius and Surface Area: Assume That The Radius R Of A Sphere Is Expanding

As the radius of a sphere increases, so does its surface area. The surface area of a sphere is given by the formula 4πr², where r is the radius of the sphere. This means that the surface area of a sphere is proportional to the square of its radius.

The implications of an expanding surface area on the sphere’s properties are numerous. For example, the sphere’s volume will increase as its surface area increases. Additionally, the sphere’s density will decrease as its surface area increases.

Implications of an Expanding Surface Area on the Sphere’s Properties

• The sphere’s volume will increase as its surface area increases.
• The sphere’s density will decrease as its surface area increases.

Expanding Radius and Volume

As the radius of a sphere increases, so does its volume. The volume of a sphere is given by the formula 4/3πr³, where r is the radius of the sphere. This means that the volume of a sphere is proportional to the cube of its radius.

The implications of an expanding volume on the sphere’s properties are numerous. For example, the sphere’s mass will increase as its volume increases. Additionally, the sphere’s density will decrease as its volume increases.

Implications of an Expanding Volume on the Sphere’s Properties, Assume that the radius r of a sphere is expanding

• The sphere’s mass will increase as its volume increases.
• The sphere’s density will decrease as its volume increases.

Expanding Radius and Density

As the radius of a sphere increases, its density decreases. The density of a sphere is given by the formula m/V, where m is the mass of the sphere and V is the volume of the sphere. This means that the density of a sphere is inversely proportional to its volume.

The implications of an expanding radius on the sphere’s density are numerous. For example, a sphere with a larger radius will have a lower density than a sphere with a smaller radius.

Implications of an Expanding Radius on the Sphere’s Density

• A sphere with a larger radius will have a lower density than a sphere with a smaller radius.

Expanding Radius and Pressure

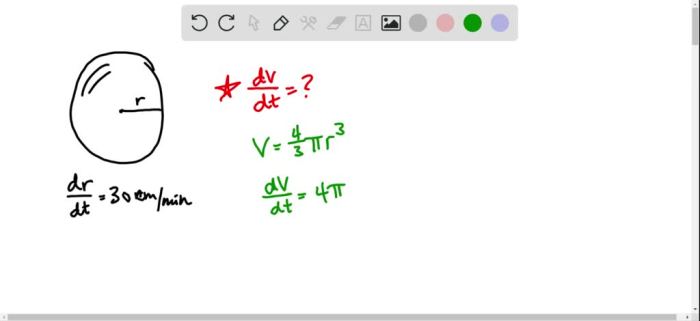
As the radius of a sphere increases, the pressure within the sphere decreases. The pressure within a sphere is given by the formula P = F/A, where P is the pressure, F is the force, and A is the area.

This means that the pressure within a sphere is inversely proportional to the area of the sphere.

The implications of an expanding radius on the pressure within the sphere are numerous. For example, a sphere with a larger radius will have a lower pressure than a sphere with a smaller radius.

Implications of an Expanding Radius on the Pressure within the Sphere

• A sphere with a larger radius will have a lower pressure than a sphere with a smaller radius.

FAQ

What is the relationship between the surface area of a sphere and its radius?

The surface area of a sphere is directly proportional to the square of its radius (A = 4πr^2).

How does the volume of a sphere change as its radius expands?

The volume of a sphere is directly proportional to the cube of its radius (V = 4/3πr^3).

What is the effect of an expanding radius on the density of a sphere?

As the radius of a sphere expands, its density decreases (ρ = m/V, where m is mass and V is volume).

How does the pressure within a sphere change as its radius expands?

The pressure within a sphere is inversely proportional to the radius (P = 2T/r, where T is tension).